The Pushover Analysis, explained in its Simplicity

Introduction

            One of the emerging fields in seismic design of structures is the Performance Based Design. The subject is still in the realm of research and academics, and is only slowly emerging out into the practitioner’s arena. Seismic design is slowly transforming from a stage where a linear elastic analysis for a structure was sufficient for both its elastic and ductile design, to a stage where a specially dedicated non-linear procedure is to be done, which finally influences the seismic design as a whole.

            The basis for the linear approach lies in the concept of the Response Reduction factor R. When a structure is designed for a Response Reduction factor of, say, R = 5, it means that only 1/5^th of the seismic force is taken by the Limit State capacity of the structure. Further deflection is in its ductile behaviour and is taken by the ductile capacity of the structure. In Reinforced Concrete (RC) structures, the members (ie., beams and columns) are detailed such as to make sure that the structure can take the full impact without collapse beyond its Limit State capacity up to its ductile capacity. In fact we never analyse for the ductile part, but only follow the reinforcement detailing guidelines for the same. The drawback is that the response beyond the limit state is neither a simple extrapolation, nor a perfectly ductile behaviour with pre-determinable deformation capacity. This is due to various reasons: the change in stiffness of members due to cracking and yielding, P-delta effects, change in the final seismic force estimated, etc. Although elastic analysis gives a good indication of elastic capacity of structures and shows where yielding might first occur, it cannot account for redistribution of forces during the progressive yielding that follows and predict its failure mechanisms, or detect possibility and location of any premature failure. A non-linear static analysis can predict these more accurately since it considers the inelastic behaviour of the structure. It can help identify critical members likely to reach critical states during an earthquake for which attention should be given during design and detailing.

            The need for a simple method to predict the non-linear behaviour of a structure under seismic loads saw light in what is now popularly known as the Pushover Analysis (PA). It can help demonstrate how progressive failure in buildings really occurs, and identify the mode of final failure. Putting simply, PA is a non-linear analysis procedure to estimate the strength capacity of a structure beyond its elastic limit (meaning Limit State) up to its ultimate strength in the post-elastic range. In the process, the method also predicts potential weak areas in the structure, by keeping track of the sequence of damages of each and every member in the structure (by use of what are called ‘hinges’ they hold).

Pushover vs Conventional Analysis

            In order to understand PA, the best approach would be to first see the similarities between PA and the conventional seismic analysis (SA), both Seismic Coefficient and Response Spectrum methods described in IS:1893-2002 for SA, which most of the readers are familiar with, and then see how they are different: 

• Both SA and PA apply lateral load of a predefined vertical distribution pattern on the structure. In SA, the lateral load is distributed either parabolically (in Seismic Coefficient method) or proportional to the modal combination (in the direct combination method of Response Spectrum). In PA, the distribution is proportional to height raised to the power of ‘k’, where k (equivalent to ‘2’ in the equation under Cl. 7.7.1 in IS:1893-2002) can be equal to 0 (uniform distribution), 1 (the inverted triangle distribution), 2 (parabolic distribution as in the seismic coefficient method) or a calculated value between 1 and 2, the value of k being based on the time period T of the structure, as per the FEMA 356 (where k is given a value of 2 if T ≥ 2.5 seconds, a value of 1 if T ≤ 0.5 seconds and interpolated for intermediate values of T). The distribution can also be proportional to either the first mode shape, or a combination of modes.

• In both SA and PA, the maximum lateral load estimated for the structure is calculated based on the fundamental time period of the structure.

 

And the last point above is precisely where the difference starts. While in SA the initial time period is taken to be a constant (equal to its initial value), in PA this is continuously re-calculated as the analysis progresses. The differences between the procedures are as follows :

• SA uses an elastic model, while PA uses a non-linear model. In the latter this is incorporated in the form of non-linear hinges inserted into an otherwise linear elastic model which one generates using a common structural analysis & design software package (like SAP2000 or STAAD.Pro), having facilities for PA.

The hinges

            Hinges are points on a structure where one expects cracking and yielding to occur in relatively higher intensity so that they show high flexural (or shear) displacement, as it approaches its ultimate strength under cyclic loading. These are locations where one expects to see cross diagonal cracks in an actual building structure after a seismic mayhem, and they are found to be at the either ends of beams and columns, the ‘cross’ of the cracks being at a small distance from the joint – that is where one is expected to insert the hinges in the beams and columns of the corresponding computer analysis model. Hinges are of various types – namely, flexural hinges, shear hinges and axial hinges. The first two are inserted into the ends of beams and columns. Since the presence of masonry infills have significant influence on the seismic behaviour of the structure, modelling them using equivalent diagonal struts is common in PA, unlike in the conventional analysis, where its inclusion is a rarity. The axial hinges are inserted at either ends of the diagonal struts thus modelled, to simulate cracking of infills during analysis.

            Basically a hinge represents localised force-displacement relation of a member through its elastic and inelastic phases under seismic loads. For example, a flexural hinge represents the moment-rotation relation of a beam of which a typical one is as represented in Fig.1. AB represents the linear elastic range from unloaded state A to its effective yield B, followed by an inelastic but linear response of reduced (ductile) stiffness from B to C. CD shows a sudden reduction in load resistance, followed by a reduced resistance from D to E, and finally a total loss of resistance from E to F. Hinges are inserted in the structural members of a framed structure typically as shown in Fig.2. These hinges have non-linear states defined as ‘Immediate Occupancy’ (IO), ‘Life Safety’ (LS) and ‘Collapse Prevention’ (CP) within its ductile range. This is usually done by dividing B-C into four parts and denoting IO, LS and CP, which are states of each individual hinges (in spite of the fact that the structure as a whole too have these states defined by drift limits). There are different criteria for dividing the segment BC. For instance, one such specification is at 10%, 60%, and 90% of the segment BC for IO, LS and CP respectively ( Inel & Ozmen, 2006).

 

Fig.1: A Typical Flexural Hinge Property, showing IO (Immediate Occupancy), LS (Life Safety) and CP (Collapse Prevention) 

Fig.2: Typical Locations of Hinges in a Structural Model

The two stage design approach

            Although hinge properties can be obtained from charts of average values included in FEMA356, ATC-40 and FEMA 440 (which are only rough estimates), for accurate results one requires the details of reinforcement provided in order to calculate exact hinge properties (using concrete models such as the Confined Mander model available in the SAP2000 software package). And one has to design the structure in order to obtain the reinforcement details. This means that PA is meant to be a second stage analysis. Thus the emerging methodology to an accurate seismic design is: (1) first a linear seismic analysis based on which a primary structural design is done; (2) insertion of hinges determined based on the design and then (3) a pushover analysis, followed by (4) modification of the design and detailing, wherever necessary, based on the latter analysis.

• On SA, the analysis results are always the elastic (limit state) forces (moment, shear and axial forces) to be designed for. In PA, in the global sense, it is the base shear (Vb) vs roof top displacement (Δ_{roof top}, taken as displacement of a point on the roof, located in plan at the centre of mass), plotted up to the termination of the analysis. At a local level, it is the hinge states to be examined and decided on the need for its redesign or a retrofit.

            PA can be useful under two situations: When an existing structure has deficiencies in seismic resisting capacity (due to either omission of seismic design when built, or the structure becoming seismically inadequate due to a later upgradation of the seismic codes) is to be retrofitted to meet the present seismic demands, PA can show where the retrofitting is required and how much. In fact this was what PA was originally developed for, and for which it is still widely used. For a building in its design phase, PA results help scrutinise and fine tune the seismic design based on SA, which is slowly becoming more of a standard procedure for large critical structures.

• SA, being a linear analysis, is done independently for dead and live loads, and the results added up to give the design forces. But since PA is non-linear, the gravity loads and the lateral load cases are applied sequentially in a single analysis.

• In SA, the loads are factored, since the results are for the design, but since PA is done to simulate the behaviour under actual loads, the loads applied are not factored. Thus in a PA, the gravity loads are applied in accordance with Cl.7.3.3 and Table 8 of IS:1893-2002, giving a combination of [DL + 0.25 LL_{(≤3kN/sq.m)} + 0.5 LL_(>3kN/sq.m)] – where DL denotes Dead Loads and LL, Live Load.

• In SA, the lateral load of a calculated intensity is applied in whole – in one shot. In PA, structure model (ie., the computer model for analysis) is gently ‘pushed over’ by a  monotonically increasing lateral load, applied in steps up to a predetermined value or state.

            This predetermined value or state depends on the method used. One is the Displacement Coefficient Method (DCM) of FEMA 356, where a Target Displacement is calculated to which the structure is ‘pushed’. Eurocode 8 (EN 1998-1, 2003) also follows the same approach. The other is the Capacity Spectrum Method (CSM) of ATC-40, where the load is incremented and checked at each stage, until what is called the ‘Performance Point’ condition is reached. FEMA 440 presents improvements in the procedure of both these methods. In this article, only the CSM (as described in ATC-40) is dealt with, since it is found to be more suitable than DCM for RC structures.

The Single Degree of Freedom idealization

            One of the fundamental simplifications underlying the concept of PA is that it considers the structure as a single degree of freedom (SDOF) system, which in reality it hardly is. And that means the structure model, with numerous joints with lumped masses, is assumed to be equivalent to a single vertical strut fixed at bottom with a single (but considerable) mass lumped at the top. This makes one aspect of the procedure ignore that the structure has numerous joints with different values of damping (depending on the level of damage each suffers), leaving it with just a single global value to deal with. Equations have been developed (ATC-40, FEMA 440) to arrive at this ‘equivalent’ damping ratio β, and also time period T (both continuously changing due to the weakening of hinges in course of the analysis) at any particular point in course of the progress of the analysis, having known only the instantaneous Δ_{roof top} and Vb of the structure.

The Acceleration Displacement Response Spectra

            Another of the innovative concepts incorporated in the PA is the Acceleration Displacement Response Spectra (ADRS) representation, which merges the Vb vs Δ_{roof top} plot with the Response Spectrum (RS) curve. This is possible due to a relation connecting Vb, Δ_{roof top} and T. First the Vb vs Δ_{roof top} cartesian has to be transformed to what is called spectral acceleration (Sa) vs spectral displacement (Sd) using the relations (ATC-40, 1996)

where M_k, P_k and φ_k,rooftop (using the notation of IS:1893-2002) are modal mass, mode participation factor and modal amplitude at rooftop respectively for the first mode (k=1). M and W are the total mass and weight of the building. This is effectively converting the acceleration and displacement of the building to that of the equivalent SDOF System. Next the RS graph, having axes Sa and T has to be converted using the relation in ATC-40

Thus T, which was along the x-axis in the RS curve, is marked as radial lines in the transformed plot (Fig.3). Using the above relation, the time period T represented by any radial line drawn from the origin through the point (Sd, Sa) can be found. The two transformed plots, one that of Vb vs Δ_{roof top} and the other the RS curve – now known as the capacity and demand curves respectively – can be superimposed to get the ADRS plot. 

Fig.3: ADRS representation of  the Response Spectrum curve

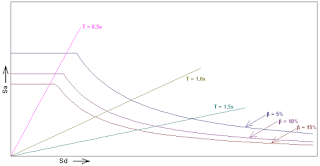
            The PA has not been introduced in the Indian Standard code yet. However the procedure described in ATC-40 can be adapted for the seismic parameters of IS:1893-2002. The RS curve in ATC-40 is described by parameters Ca and Cv, where the curve just as in IS:1893-2002, is having a flat portion of intensity 2.5 Ca and a downward sloping portion described by Cv/T (Fig.4a). The seismic force in IS:1893-2002 is represented by (ZI)/(2R)*(Sa/g), where Sa/g is obtained from the RS curve which on the other hand is represented by 2.5 in the flat portion and the downward sloping portion by 1/T, 1.36/T and 1.67/T for hard, medium and soft soils respectively (Fig.4b). On comparison it can be inferred that Ca = Z/2 and Cv is either of Z/2, 1.36∙Z/2 and 1.67∙Z/2 for hard, medium and soft soils respectively, for DBE (Design Base Earthquake – which is the one meant for design). Here ‘I’ (the importance factor as per Table 6 of IS:1893-2002) is not considered, since in PA, the criteria of importance of the structure is taken care of by the performance levels (of IO, LS and CP) instead. R is also not considered since PA is always done for the full lateral load.  

Fig.4: Response Spectrum curve (a) described in ATC-40 and (b) defined in IS:1893-2002, shown here for DBE, Zone-III (not considering I and R factors), Medium soil 

Step by step through each method

            Now let’s first see what’s actually happening in the SA procedure and then trace the progress of a PA from beginning to end, both using plots of Vb vs Δ_{roof top} and RS curve in its separate and uncombined form and also their transformed and super-positioned ADRS plot.

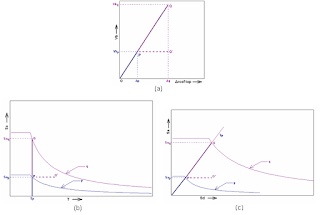
            In SA, the maximum DBE force acting on the structure is (Z/2)*(Sa/g), (not considering ‘I’) with Sa/g corresponding to the estimated time period. Its envelop is the RS curve marked q in Fig.5b, whereas the RS curve for the Limit State design is plotted in terms of (Z/2R)*(Sa/g), and is marked as curve p. Fig.5a shows the Vb vs Δ_{roof top} displacement. Now assume a structure (Fig.7a) subjected to a SA. In Fig.5a, the point P represents the Vb and Δ_{roof top} for the design lateral load (ie., of 1/R times full load) while Q represents the same for the full load, had the building been fully elastic (and Q' for a perfectly-elastic perfectly-ductile structure). The slope of the line OP represents the stiffness of the structure in a global sense. Since the analysis is linear, the stiffness remains same throughout the analysis, with Q being an extension of OP. The same is represented in Fig.5b where, for the time period Tp of the structure, the full load is represented by Q, and the design force by P.  The ADRS representation of SA is as in Fig.5c.

 

Fig.5: (a) Vb vs Δ_{roof top} plot, (b) Response spectrum and (c) ADRS plot for conventional seismic analysis

Now we shall see how differently the PA approaches the same parameters, represented by Fig.6a and 6b. The segment OA in Fig.6a is equivalent to OP in Fig.5a, with the slope representing the global stiffness in its elastic range. The same is represented by OA in Fig.6b, with time period Ta, curve ‘a’ representing the RS curve and Sa_a is the lateral load demand, in its elastic range. The Fig.6c shows the ADRS representation. Fig.7a shows the structure in this stage. As the analysis progresses, the lateral load is steadily increased beyond its elastic limit of A, and the first hinges are formed (ie., the inserted hinges starts to yield, Fig.7b). This decreases the overall stiffness of the structure, which in turn increases T and β. This is represented by the segment AB in the plots. The decrease in the secant stiffness of point B (ie., the slope of line OB, not shown) from that of point A in Fig.6a and 6c shows the change in stiffness, whereas the change in the x-axis value of point B from that of point A in Fig.6b shows the shift of time period from Ta to Tb. This is also represented by the angular shift from Ta to Tb in Fig.6c. The increase in β of the structure calls for a corresponding decrease in the RS curve, reduced by a factor calculated using β (similar to that found in Table 3 of IS:1893-2002), which has thus come down from curve a to b in Fig.6b and 6c.

With the new time period Tb and RS curve b, the lateral load expected to act on the structure has come down from Sa_a to Sa_b. The analysis still needs to progress since the actual force being applied on the structure ~Vb_b has not reached the total force Sa_b expected at this stage (~Vb_b in Fig.6c is Vb_b of Fig.6a transformed using Eq.1). As the base shear Vb is further increased monotonically, more hinges are formed and the existing hinges have further yielded in its non-linear phase (Fig.7c), represented by point C in Fig.6a, 6b and 6c. This has further reduced the stiffness (the slope of OC – not marked – in  Fig.6a and 6c), and increased T (from Tb to Tc in Fig.6b and 6c). Finally the point C is where the capacity curve OABC extending upwards with the increase in lateral push meets the demand curve in Fig.6c, which was simultaneously descending down to curve c  due to increase in β. Thus C is the point where the total lateral force expected Sa_c is same as the lateral force applied ~Vb_c – this point is known as the Performance Point. It is also defined as the point where the ‘locus of the Performance Point’, the line connecting Sa_a, Sa_b and Sa_c (the load demands for points A, B, C in Fig.6c), intersects the capacity curve (which is, in general, the method used by software packages to determine the Performance Point). Of course, it can happen that if the structure is seismically weak, it can reach its collapse mechanism before the capacity curve can meet the descending demand curve, denying the structure of a Performance Point.

 

Fig.6: (a) Vb vs Δ_{roof top} plot, (b) Response spectrum and (c) ADRS plot for pushover analysis

Once the Performance Point is found, the overall performance of the structure can be checked to see whether it matches the required performance level of IO, LS or CP, based on drift limits specified in ATC-40 which are 0.01h, 0.02h and 0.33(Vb/W)∙h respectively (h being the height of the building). The performance level is based on the importance and function of the building. For example, hospitals and emergency services buildings are expected to meet a performance level of IO. In fact these limits are more stringent than those specified in IS:1893-2002. The ‘Limit State’ drifts of 0.004 specified in the latter, when accounted for R (= 5 for ductile design) and I (taken as 1.5 for important structures which demand an IO performance level) gives 0.004∙R/I = 0.0133, which is more relaxed than the 0.01 allowed in ATC-40. This 0.004∙R/I may be taken as the IS:1893-2002 limits for pushover drift, where I takes the value corresponding to Important and Ordinary structures for limits of IO and LS respectively.

             The next step is to review the hinge formations at Performance Point. One can see the individual stage of each hinge, at its location. Tables are obtained showing the number of hinges in each state, at each stage, based on which one decides which all beams and columns to be redesigned. The decision depends whether the most severely yielded hinges are formed in beams or in columns, whether they are concentrated in a particular storey denoting soft story, and so on.

Fig.7: Structure model at (a) stage ‘A’, (b) stage ‘B’ and (c) stage ‘C’. Also shown in is the lateral load pattern, and colour code for hinge states of IO (Immediate Occupancy), LS (Life Safety) and CP (Collapse Prevention)

Example of a building analysis

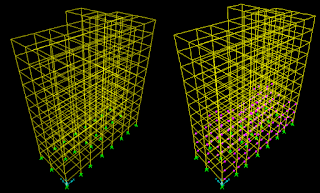
            Presented in this section are the results of a pushover analysis done on a 10 storey RC building of a shopping complex (Jisha, 2008) (Fig.8) using the structural package of SAP2000. In the model, beams and columns were modelled using frame elements, into which the hinges were inserted. Diaphragm action was assigned to the floor slabs to ensure integral lateral action of beams in each floor. Although analysis was done in both transverse and longitudinal directions, only the results of the former are discussed here.

 

Fig.8: A view of the computer model of building being analysed

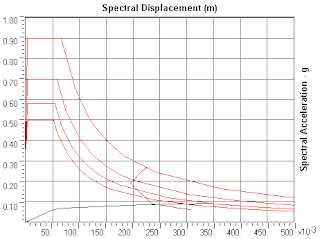
The lateral load was applied in pattern of that first mode shape in the transverse direction of the building, with an intensity for DBE as per IS:1893-2002, corresponding to zone-III in hard soil. Fig.9 shows the ADRS plot in which the Sa and Sd at Performance Point are 0.085g and 0.242m. The corresponding Vb and Δ_{roof top} are 1857.046 kN and 0.287m. The value of effective T is 3.368s. The effective β at that level of the demand curve which met the Performance Point is 26%.

 

Fig.9: ADRS plot for the analysis (Capacity curve in green, demand curves in red, and locus of Performance Point in dark yellow)

Table 1: Hinge states in each step of the pushover analysis (see Fig.1 for notations)

 

Step	Δroof top (m)	Vb (kN)	Hinge States								Total Hinges
			A to B	B to IO	IO to LS	LS to CP	CP to C	C to D	D to E	> E
0	0	0	1752	0	0	0	0	0	0	0	1752
1	0.058318	1084.354	1748	4	0	0	0	0	0	0	1752
2	0.074442	1348.412	1670	82	0	0	0	0	0	0	1752
3	0.089645	1451.4	1594	158	0	0	0	0	0	0	1752
4	0.26199	1827.137	1448	168	136	0	0	0	0	0	1752
5	0.41105	2008.48	1384	144	136	88	0	0	0	0	1752
6	0.411066	1972.693	1384	146	136	86	0	0	0	0	1752
7	0.411082	1576.04	1376	148	136	39	0	0	53	0	1752
8	0.411098	1568.132	1376	148	136	37	0	0	55	0	1752
9	0.411114	1544.037	1375	149	136	31	0	0	61	0	1752
10	0.40107	1470.133	1375	149	136	31	0	0	61	0	1752

   

Table.1 shows the hinge state details at each step of the analysis. It can be seen that for the Performance Point, taken as step 5 (which actually lies between steps 4 and 5), 95% of hinges are within LS and 88% within IO performance level. Fig.10a to 10e shows the hinge states during various stages in course of the analysis. A Δ_{roof top} of 0.287 m, with the height of the building up to rooftop h (which excludes the staircase tower room) being 36.8m, gives a Δ_{roof top} to h ratio of 0.0078 (in an average sense) which lies within the performance level of IO.

(a)                                            (b)

(c)                                            (d)

    (e)

Fig.10: Hinge states in the structure model at (a) step 0, (b) step 3, (c) step 5, (d) step 8 and (e) step 10 during the pushover analysis, with colour codes of hinge states

Limitations

            As such the method appears complete and sound, yet there are many aspects which are unresolved, which include incorporation of torsional effects of buildings, problems faced due to use of diagonal struts, etc. The most addressed (but yet unresolved) issue is that the procedure basically takes into account only the fundamental mode (as can be seen in the procedure for transforming Vb and Δ_{roof top} to Sa and Sd,  explained earlier), assuming it to be the predominant response and does not consider effects of higher modes. The discrepancies due to this start to be felt for buildings with T over 1 second.   Although many research papers proposed various solutions on how to incorporate higher modes (more effectively than a mere combination of lateral loads corresponding to each mode), a method is yet to be set standard, and included in the software packages. Moreover, the PA method as such is yet to be incorporated in the Indian Standards.

Conclusion & Acknowledgement

            What I have intended here is to explain the method with as much simplicity as I could so as to introduce the basic concepts to those who are already familiar with the conventional seismic analyses. I hope I have, at least to some extend, fulfilled my aim. Of course, there are many aspects which this article has not touched – like obtaining hinge properties from section details, incorporating effects of soil structure interaction, deciding on different pushover analysis parameters, method modelling shear walls and flat slabs with hinges, etc. – since this isn’t meant to deal with the procedure to that extend. The example of pushover analysis presented in this article is taken from the academic work by Mrs. Jisha S. V., a former PG student in Structural Engineering, which is gratefully acknowledged.

Slide presentation & Paper
     You may find a slide presentation, dealing with the topic more elaborately at http://www.slideshare.net/rahulleslie/the-pushover-analysis-from-basics-rahul-leslie. 
           You may also find the published copy of the paper (as PDF) at https://www.researchgate.net/publication/323607343_The_Pushover_Analysis_in_its_Simplicity

Citation
     Citations may be referenced as: Rahul Leslie, “The Pushover Analysis in its Simplicity”, Jun 2012, Civil Engineering and Construction Review magazine, India. pp. 118-126

-- Rahul Leslie, Assistant Director, Buildings Design, DRIQ, Kerala PWD, Trivandrum, India

Reference:

-          IS 1893 (Part 1)–2002, “Indian Standard Criteria for Earthquake Resistant Design of Structures, Part 1: General Provision and Buildings”, Bureau of Indian Standards, New Delhi.

-          FEMA 356 (2000) “Prestandard and Commentary for the Seismic Rehabilitation of Buildings”, Federal Emergency Management Agency, Washington, DC, USA.

-          ATC-40 (1996) “Seismic Analysis and Retrofit of Concrete Buildings”, vol. I, Applied Technology Council, Redwood City, CA, USA.

-          FEMA-440 (2205) “Improvement of Nonlinear static seismic analysis procedures”, Federal Emergency Management Agency, Washington, DC, U.S.A.

-          EN 1998-1:2003, “Eurocode 8: Design of structures for earthquake resistance - Part 1: General rules, seismic actions and rules for buildings”, European Committee for Standardization, Management Centre: rue de Stassart, 36 B-1050 Brussels.

-          Mehmet Inel & Hayri Baytan Ozmen, "Effects of plastic hinge properties in nonlinear analysis of reinforced concrete buildings", Engineering Structures 28 (2006) pg. 1494–1502 (http://www.elsevier.com/locate/engstruct).

-          SAP2000. “Integrated software for structural analysis and design”, Computers and Structures Inc., Berkeley, CA, USA.

-          Jisha S. V. (2008), Mini Project Report “Pushover Analysis”, Department of Civil Engineering, T. K. M. College of Engineering, Kollam, Kerala.

RAHUL LESLIE'S BLOG POSTS:-

List of blogs